In the previous post (https://statcompute.wordpress.com/2018/08/26/adjacent-categories-and-continuation-ratio-logit-models-for-ordinal-outcomes), we’ve shown alternative models for ordinal outcomes in addition to commonly used Cumulative Logit models under the proportional odds assumption, which are also known as Proportional Odds model. A potential drawback of Proportional Odds model is the lack of flexibility and the restricted assumption of proportional odds, of which the violation might lead to the model mis-specification. As a result, Cumulative Logit models with more flexible assumptions are called for.
In the example below, I will first show how to estimate credit ratings with a Cumulative Logit model under the proportional odds assumption with corporate financial performance measures, expressed as Logit(Y <= j) = A_j – X * B, where A_j depends on the category j.
pkgs <- list("maxLik", "VGAM")
sapply(pkgs, require, character.only = T)
data(data_cr, envir = .GlobalEnv, package = "mvord")
data_cr$RATING <- pmax(data_cr$rater1, data_cr$rater2, na.rm = T)
x <- c("LR", "LEV", "PR", "RSIZE", "BETA")
# LR : LIQUIDITY RATIO
# LEV : LEVERAGE RATIO
# PR : PROFITABILITY RATIO
# RSIZE: LOG OF RELATIVE SIZE
# BETA : SYSTEMATIC RISK
y <- "RATING"
df <- data_cr[!is.na(data_cr[, y]), c(x, y)]
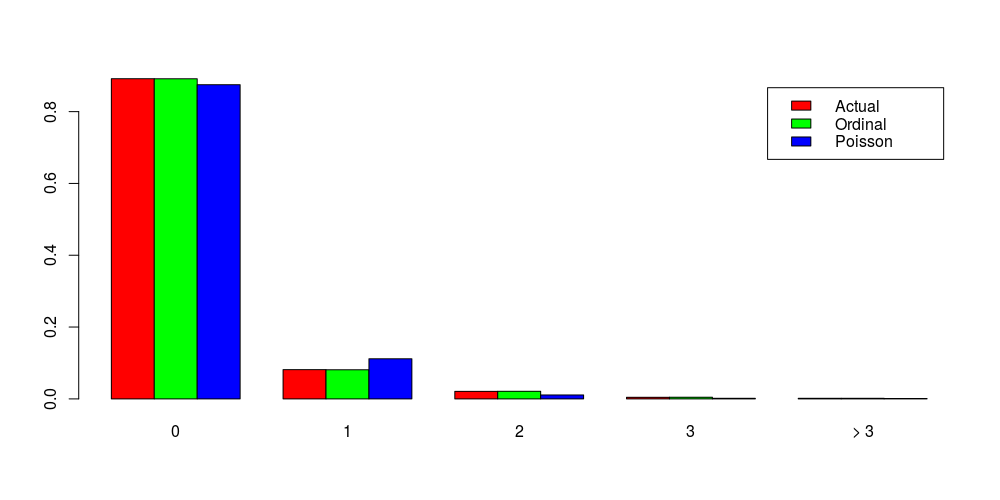
table(df[, y]) / length(df[, y])
# A B C D E
# 0.1047198 0.1681416 0.3023599 0.2994100 0.1253687
### CUMULATIVE LOGIT MODEL ASSUMED PROPORTIONAL ODDS ###
# BELOW IS THE SIMPLER EQUIVALENT:
# vglm(RATING ~ LR + LEV + PR + RSIZE + BETA, data = df, family = cumulative(parallel = T))
ll1 <- function(param) {
plist <- c("a_A", "a_B", "a_C", "a_D", "b_LR", "b_LE", "b_PR", "b_RS", "b_BE")
sapply(1:length(plist), function(i) assign(plist[i], param[i], envir = .GlobalEnv))
XB_A <- with(df, a_A - (b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_B <- with(df, a_B - (b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_C <- with(df, a_C - (b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_D <- with(df, a_D - (b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
prob_A <- 1 / (1 + exp(-XB_A))
prob_B <- 1 / (1 + exp(-XB_B)) - prob_A
prob_C <- 1 / (1 + exp(-XB_C)) - prob_A - prob_B
prob_D <- 1 / (1 + exp(-XB_D)) - prob_A - prob_B - prob_C
prob_E <- 1 - prob_A - prob_B - prob_C - prob_D
CAT <- data.frame(sapply(c("A", "B", "C", "D", "E"), function(x) assign(x, df[, y] == x)))
LH <- with(CAT, (prob_A ^ A) * (prob_B ^ B) * (prob_C ^ C) * (prob_D ^ D) * (prob_E ^ E))
return(sum(log(LH)))
}
start1 <- c(a_A = 0, a_B = 2, a_C = 3, a_D = 4, b_LR = 0, b_LE = 0, b_PR = 0, b_RS = 0, b_BE = 0)
summary(m1 <- maxLik(logLik = ll1, start = start1))
# Estimate Std. error t value Pr(t)
#a_A 15.53765 0.77215 20.123 <2e-16 ***
#a_B 18.26195 0.84043 21.729 <2e-16 ***
#a_C 21.61729 0.94804 22.802 <2e-16 ***
#a_D 25.88787 1.10522 23.423 <2e-16 ***
#b_LR 0.29070 0.11657 2.494 0.0126 *
#b_LE 0.83977 0.07220 11.631 <2e-16 ***
#b_PR -5.10955 0.35531 -14.381 <2e-16 ***
#b_RS -2.18552 0.09982 -21.895 <2e-16 ***
#b_BE 3.26811 0.21696 15.063 <2e-16 ***
In the above output, the attribute “liquidity ratio” is somewhat less significant than the other, implying a potential opportunity for further improvements by relaxing the proportional odds assumption. As a result, I will try a different class of Cumulative Logit models, namely (unconstrained) Partial-Proportional Odds models, that would allow non-proportional odds for a subset of model attributes, e.g. LR in our case. Therefore, the formulation now becomes Logit(Y <= j) = A_j – X * B – Z * G_j, where both A_j and G_j vary by the category j.
### CUMULATIVE LOGIT MODEL ASSUMED UNCONSTRAINED PARTIAL-PROPORTIONAL ODDS ###
# BELOW IS THE SIMPLER EQUIVALENT:
# vglm(RATING ~ LR + LEV + PR + RSIZE + BETA, data = df, family = cumulative(parallel = F ~ LR))
ll2 <- function(param) {
plist <- c("a_A", "a_B", "a_C", "a_D", "b_LRA", "b_LRB", "b_LRC", "b_LRD", "b_LE", "b_PR", "b_RS", "b_BE")
sapply(1:length(plist), function(i) assign(plist[i], param[i], envir = .GlobalEnv))
XB_A <- with(df, a_A - (b_LRA * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_B <- with(df, a_B - (b_LRB * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_C <- with(df, a_C - (b_LRC * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_D <- with(df, a_D - (b_LRD * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
prob_A <- 1 / (1 + exp(-XB_A))
prob_B <- 1 / (1 + exp(-XB_B)) - prob_A
prob_C <- 1 / (1 + exp(-XB_C)) - prob_A - prob_B
prob_D <- 1 / (1 + exp(-XB_D)) - prob_A - prob_B - prob_C
prob_E <- 1 - prob_A - prob_B - prob_C - prob_D
CAT <- data.frame(sapply(c("A", "B", "C", "D", "E"), function(x) assign(x, df[, y] == x)))
LH <- with(CAT, (prob_A ^ A) * (prob_B ^ B) * (prob_C ^ C) * (prob_D ^ D) * (prob_E ^ E))
return(sum(log(LH)))
}
start2 <- c(a_A = 0.1, a_B = 0.2, a_C = 0.3, a_D = 0.4, b_LRA = 0, b_LRB = 0, b_LRC = 0, b_LRD = 0, b_LE = 0, b_PR = 0, b_RS = 0, b_BE = 0)
summary(m2 <- maxLik(logLik = ll2, start = start2))
#Estimates:
# Estimate Std. error t value Pr(t)
#a_A 15.30082 0.83936 18.229 <2e-16 ***
#a_B 18.14795 0.81325 22.315 <2e-16 ***
#a_C 21.72469 0.89956 24.150 <2e-16 ***
#a_D 25.92697 1.07749 24.062 <2e-16 ***
#b_LRA 0.12442 0.30978 0.402 0.6880
#b_LRB 0.21127 0.20762 1.018 0.3089
#b_LRC 0.36097 0.16687 2.163 0.0305 *
#b_LRD 0.31404 0.22090 1.422 0.1551
#b_LE 0.83949 0.07155 11.733 <2e-16 ***
#b_PR -5.09891 0.35249 -14.465 <2e-16 ***
#b_RS -2.18589 0.09540 -22.913 <2e-16 ***
#b_BE 3.26529 0.20993 15.554 <2e-16 ***
As shown above, under the partial-proportional odds assumption, there are 4 parameters estimated for LR, three of which are not significant and therefore the additional flexibility is not justified. In fact, AIC of the 2nd model (AIC = 1103.60) is even higher than AIC of the 1st model (AIC = 1098.18).
In light of the above observation, I will introduce the 3rd model, which is known as the Constrained Partial-Proportional Odds model and expressed as Logit(Y <= j) = A_j – X * B – Z * G * gamma_j, where A_j and gamma_j vary the category j. It is worth pointing out that gamma_j is a pre-specified fixed scalar and does not need to be estimated. Based on the unconstrained model outcome, we can set gamma_1 = 1, gamma_2 = 2, and gamma_3 = gamma_4 = 3 for LR in our case.
### CUMULATIVE LOGIT MODEL ASSUMED CONSTRAINED PARTIAL-PROPORTIONAL ODDS ###
ll3 <- function(param) {
plist <- c("a_A", "a_B", "a_C", "a_D", "b_LR", "b_LE", "b_PR", "b_RS", "b_BE")
sapply(1:length(plist), function(i) assign(plist[i], param[i], envir = .GlobalEnv))
gamma <- c(1, 2, 3, 3)
XB_A <- with(df, a_A - (gamma[1] * b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_B <- with(df, a_B - (gamma[2] * b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_C <- with(df, a_C - (gamma[3] * b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_D <- with(df, a_D - (gamma[4] * b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
prob_A <- 1 / (1 + exp(-XB_A))
prob_B <- 1 / (1 + exp(-XB_B)) - prob_A
prob_C <- 1 / (1 + exp(-XB_C)) - prob_A - prob_B
prob_D <- 1 / (1 + exp(-XB_D)) - prob_A - prob_B - prob_C
prob_E <- 1 - prob_A - prob_B - prob_C - prob_D
CAT <- data.frame(sapply(c("A", "B", "C", "D", "E"), function(x) assign(x, df[, y] == x)))
LH <- with(CAT, (prob_A ^ A) * (prob_B ^ B) * (prob_C ^ C) * (prob_D ^ D) * (prob_E ^ E))
return(sum(log(LH)))
}
start3 <- c(a_A = 1, a_B = 2, a_C = 3, a_D = 4, b_LR = 0.1, b_LE = 0, b_PR = 0, b_RS = 0, b_BE = 0)
summary(m3 <- maxLik(logLik = ll3, start = start3))
#Estimates:
# Estimate Std. error t value Pr(t)
#a_A 15.29442 0.60659 25.214 < 2e-16 ***
#a_B 18.18220 0.65734 27.660 < 2e-16 ***
#a_C 21.70599 0.75181 28.872 < 2e-16 ***
#a_D 25.98491 0.88104 29.493 < 2e-16 ***
#b_LR 0.11351 0.04302 2.638 0.00833 **
#b_LE 0.84012 0.06939 12.107 < 2e-16 ***
#b_PR -5.10025 0.33481 -15.233 < 2e-16 ***
#b_RS -2.18708 0.08118 -26.940 < 2e-16 ***
#b_BE 3.26689 0.19958 16.369 < 2e-16 ***
As shown above, after the introduction of gamma_j as the constrained scalar, the statistical significance of LR has been improved with a slightly lower AIC = 1097.64.
To be complete, I’d like to mention the last model today, which is named the Stereotype model. The idea of Stereotype models is very similar to the idea of adjacent-categories models and is to estimate Log(Y = j / Y = j+1) or more often Log(Y = j / Y = j_c), where C represents a baseline category. However, the right-hand side is expressed as Log(…) = A_j – (X * B) * phi_j, where phi_j is a hyper-parameter such that phi_1 = 1 > phi_2…> phi_max = 0. As a result, the coefficient of each model attribute could also vary by the category j, introducing more flexibility at the cost of being difficult to estimate.
### STEREOTYPE MODEL ###
# BELOW IS THE SIMPLER EQUIVALENT:
# rrvglm(sapply(c("A", "B", "C", "D", "E"), function(x) df[, y] == x)~ LR + LEV + PR + RSIZE + BETA, multinomial, data = df)
ll4 <- function(param) {
plist <- c("a_A", "a_B", "a_C", "a_D", "b_LR", "b_LE", "b_PR", "b_RS", "b_BE", "phi_B", "phi_C", "phi_D")
sapply(1:length(plist), function(i) assign(plist[i], param[i], envir = .GlobalEnv))
XB_A <- with(df, a_A - (b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_B <- with(df, a_B - phi_B * (b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_C <- with(df, a_C - phi_C * (b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
XB_D <- with(df, a_D - phi_D * (b_LR * LR + b_LE * LEV + b_PR * PR + b_RS * RSIZE + b_BE * BETA))
prob_A <- exp(XB_A) / (exp(XB_A) + exp(XB_B) + exp(XB_C) + exp(XB_D) + 1)
prob_B <- exp(XB_B) / (exp(XB_A) + exp(XB_B) + exp(XB_C) + exp(XB_D) + 1)
prob_C <- exp(XB_C) / (exp(XB_A) + exp(XB_B) + exp(XB_C) + exp(XB_D) + 1)
prob_D <- exp(XB_D) / (exp(XB_A) + exp(XB_B) + exp(XB_C) + exp(XB_D) + 1)
prob_E <- 1 - prob_A - prob_B - prob_C - prob_D
CAT <- data.frame(sapply(c("A", "B", "C", "D", "E"), function(x) assign(x, df[, y] == x)))
LH <- with(CAT, (prob_A ^ A) * (prob_B ^ B) * (prob_C ^ C) * (prob_D ^ D) * (prob_E ^ E))
return(sum(log(LH)))
}
start4 <- c(a_A = 1, a_B = 2, a_C = 3, a_D = 4, b_LR = 0.1, b_LE = 0, b_PR = 0, b_RS = 0, b_BE = 0, phi_B = 0.1, phi_C = 0.2, phi_D = 0.3)
summary(m4 <- maxLik(logLik = ll4, start = start4))
#Estimates:
# Estimate Std. error t value Pr(t)
#a_A 67.73429 2.37424 28.529 <2e-16 ***
#a_B 55.86469 1.94442 28.731 <2e-16 ***
#a_C 41.27477 1.47960 27.896 <2e-16 ***
#a_D 22.24244 1.83137 12.145 <2e-16 ***
#b_LR 0.86975 0.37481 2.320 0.0203 *
#b_LE 2.79215 0.23373 11.946 <2e-16 ***
#b_PR -16.66836 1.17569 -14.178 <2e-16 ***
#b_RS -7.24921 0.33460 -21.665 <2e-16 ***
#b_BE 10.57411 0.72796 14.526 <2e-16 ***
#phi_B 0.77172 0.03155 24.461 <2e-16 ***
#phi_C 0.52806 0.03187 16.568 <2e-16 ***
#phi_D 0.26040 0.02889 9.013 <2e-16 ***

















You must be logged in to post a comment.