Modeling Rates and Proportions in SAS – 6

5. BETA REGRESSION

Beta regression is a flexible modeling technique based upon the 2-parameter beta distribution and can be employed to model any dependent variable that is continuous and bounded by 2 known endpoints, e.g. 0 and 1 in our context. Assumed that Y follows a standard beta distribution defined in the interval (0, 1) with 2 shape parameters W and T, the density function can be specified as
F(Y) = Gamma(W + T) / (Gamma(W) * Gamma(T)) * Y ^ (W – 1) * (1 – Y) ^ (T – 1)
In the above function, while W is pulling the density toward 0, T is pulling the density toward 1. Without the loss of generality, W and T can be re-parameterized and translated into 2 other parameters, namely location parameter Mu and dispersion parameter Phi such that W = Mu * Phi and T = Phi * (1 – Mu), where Mu is the expected mean and Phi is another parameter governing the variance such that sigma ^ 2 = Mu * (1 – Mu) / (1 + Phi).

Within the framework of generalized linear models (GLM), Mu and Phi can be modeled separately with 2 overlapping or identical sets of covariates X and Z, a location sub-model for Mu and the other dispersion sub-model for Phi. Since the expected mean Mu is bounded by 0 and 1, a natural choice of the link function for location sub-model is logit such that LOG(Mu / (1 – Mu)) = X`B. With the strictly positive nature of Phi, a log function seems appropriate to serve our purpose such that LOG(Phi) = – Z`G, in which the negative sign is only for the purpose of easy interpretation such that the positive G represents a positive impact on the variance.

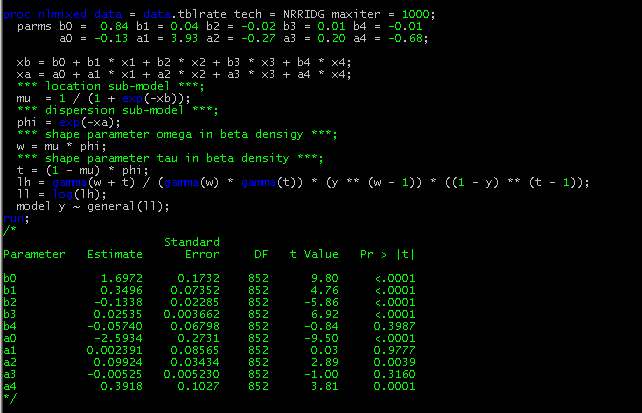
SAS does not provide the out-of-box procedure to estimate Beta regression. While GLIMMIX procedure is claimed to accommodate Beta modeling, it can only estimate a simple-form of Beta regression without the dispersion sub-model. However, with the density function of Beta distribution, it is extremely easy to model Beta regression with NLMIXED procedure by specifying the log likelihood function. In addition, for the data with a relatively small size, Beta regression estimated with NLMIXED procedure converges very well by setting initial values of parameter estimates equal to parameters from TOBIT model in the previous session.